Requirements

Kalyna’s Key Scheduler is needed to be designed to satisfy the below requirements:

• Non-linear dependence of every round key bit on every encryption key bit

• Round key independence

• High computational complexity of encryption key recovery even having all round keys

• Strength to all known cryptanalytic attacks on key schedule

• Absence of weak key worsen cryptographic properties

• Implementation simplicity (application of round transformation only)

• Partial protection from side-channel attacks

Properties

• Key Agility - less than $2.5$ - Takes $2.5$ Times less amount of time when compared to Encryption of one block.

• Non Invertible - Non-Bijective Round key dependency on the encryption master key - unlike $\text{AES}$

• Key scheduling works as a secure $\text{PRNG}$ with cryptographic properties like high uniqueness.

• Number of Round Keys $(t)$ - The number depends on the Key Size $(k)$

Algorithm

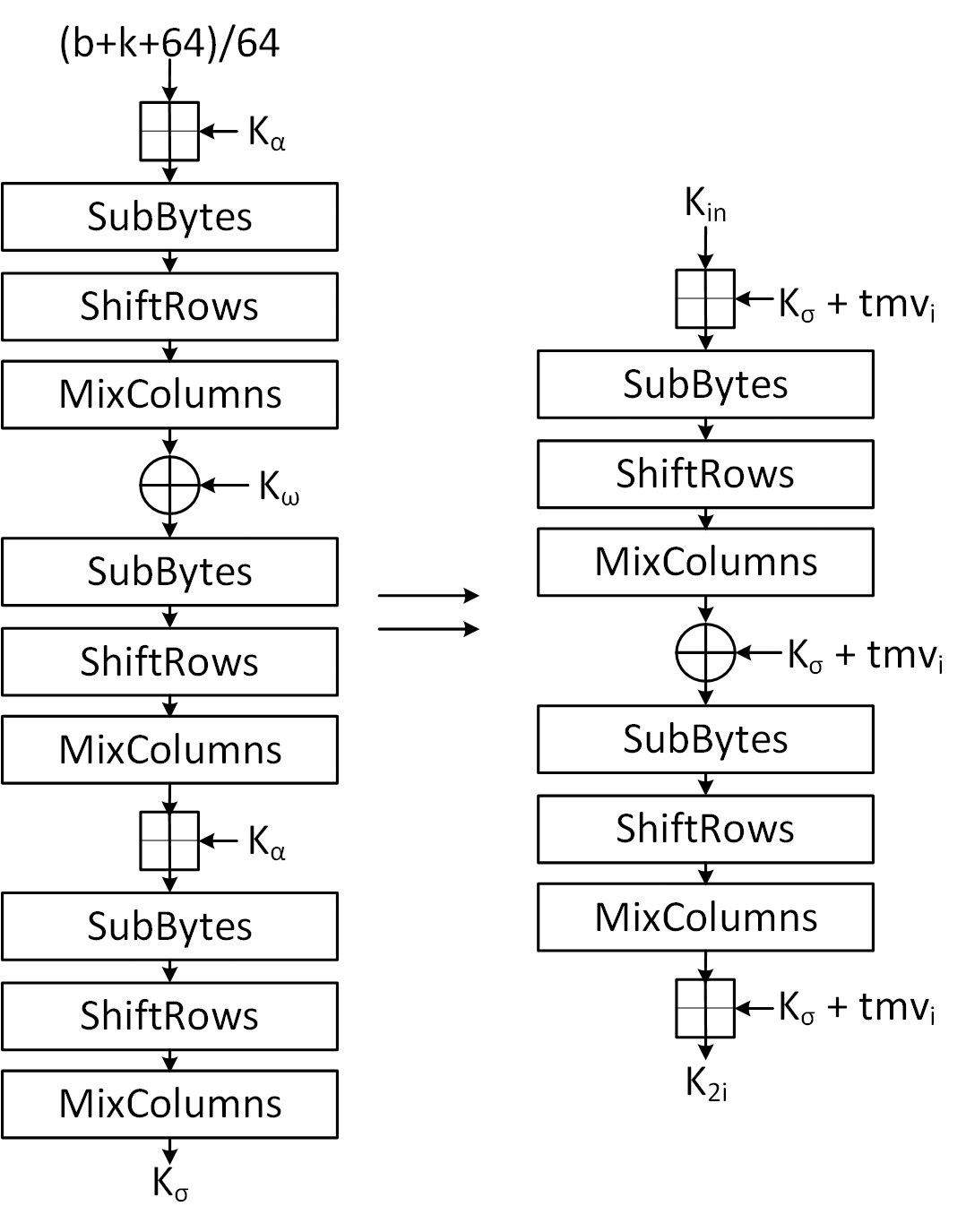
Intermediate Key $(K_\sigma)$ Generation

• Intermediate key $(K_\sigma)$ is one of the core components of Kalyna Key Expansion Algorithm as it helps in bridging the gap between the differences in Block and Key Sizes.

• It generated from the Master Key $K$ which is divided into two Blocks $K_\alpha$ and $K_\omega$ the following way
  • If Key Size $k$ is twice the Block Size $b$

    $K_\alpha$ - First/Least Significant Half amount of Columns of the Master Key $K$.

    $K_\omega$ - Later/Most Significant Half amount of Columns of the Master Key $K.$

  • If Key Size $k$ and the Block Size $b$ are same

    $K_\alpha = K_\omega = K$

  $$K={\begin{cases}K_\alpha||K_\omega&{\text{if }}k = 2b\\ K_\alpha = K_\omega & {\text{if }}k = b\end{cases}}$$

Intermediate Constant $(\theta)$

• To generate the Intermediate Key $(K_\sigma)$ we need to first generate the Intermediate Constant

• The intermediate constant is dependent on the following factors

• We make the first/Least significant byte $\mathtt{b_0}$ of the Intermediate Key equal to this constant

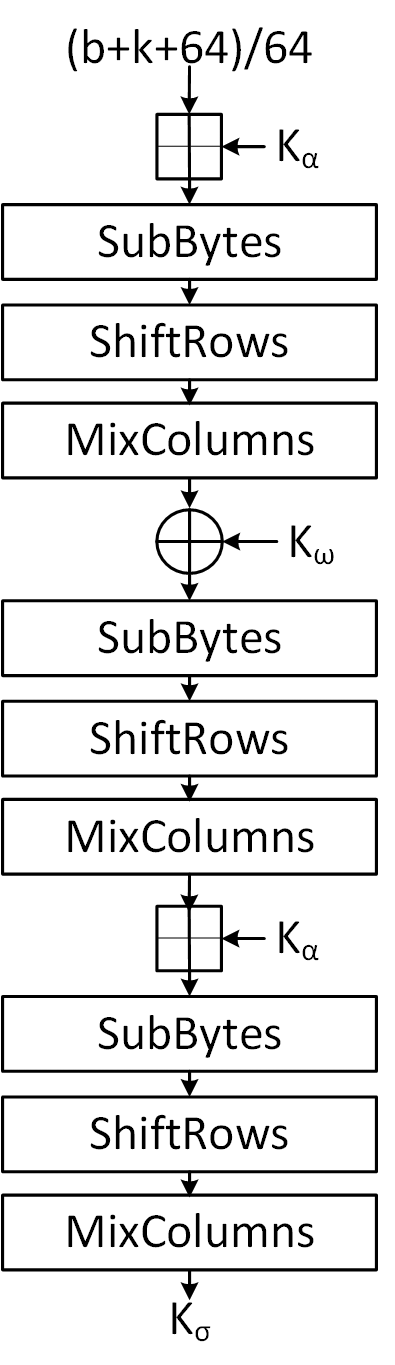
Generation

• We then do the following operations (Done from Right to left)

$\eta_b^{(K_\alpha, \theta)}$ - Addition Modulus $2^{64}$ between $K_\alpha$, Intermediate Constant $\theta$

$\pi$ - Substitution Layer

$\tau$ - Shift Rows

$\psi$ - Mix Columns

$\kappa_b^{K_\omega}$ - $\text{XOR}$ Addition with $K_\omega$ and the current state of Intermediate Key of Block Size $b$

$\eta_b^{K_\alpha}$ - Addition Modulus $2^{64}$ with $K_\alpha$ and the current state of Intermediate Key of Block Size $b$

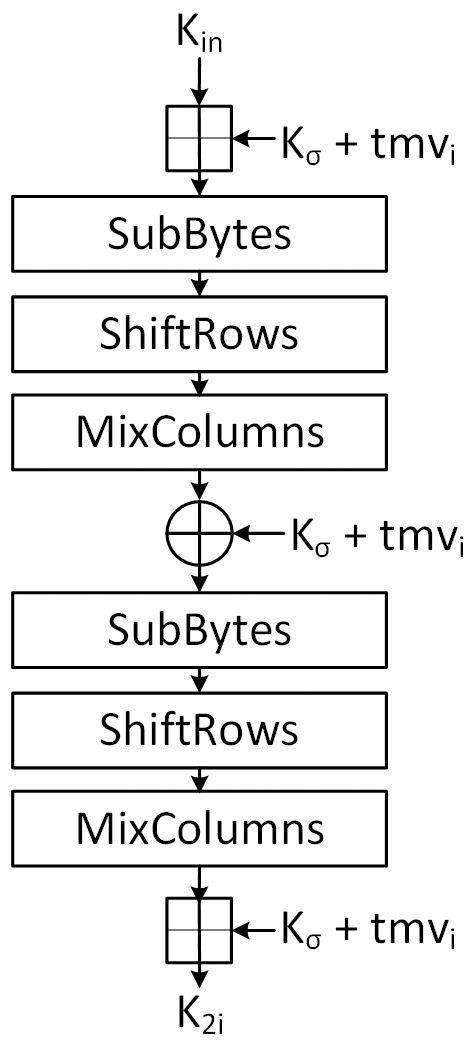
Even Round Key Generation

Initial Round Key State $(K_\text{in})$

• The Initial Round Key state $(K_\text{in})$ is used to generate the Final Even $(2i)$ Round Key

• It is calculated using the following algorithm for round number $i$.

Round Constant $(\text{tmv}_i/ \mu_i)$

• This constant changes w.r.t round number $0 \leq i \leq t$

• The constant is calculated the following way

  $$\mu_i = \mathtt{0x01}<< i \bmod 8\\ \forall i \in \{0,2,4,6,\ldots,t\}$$

• This constant is then inserted into every Even Byte $\mathtt{b_{2n}}$ of the Round Constant vector $\text{tmv}_i$ which is has the same dimensions as the Kalyna Block and then left rotated the following way

Generation

• We then do the following operations (Done from Right to left)

$\eta_b^{(K_\text{in}, K_\sigma, \text{tmv}_i)}$ - Addition Modulus $2^{64}$ between Intermediate Key $K_\sigma$, Round Constant $\text{tmv}_i$ and Initial State $K_{\text{in}}$ with Block Size $b$

$\pi$ - Substitution Layer

$\tau$ - Shift Rows

$\psi$ - Mix Columns

$\eta_b^{(K_\sigma, \text{tmv}_i)}$ - Addition Modulus $2^{64}$ between Intermediate Key $K_\sigma$, Round Constant $\text{tmv}_i$

$\kappa_b^{X}$ - $\text{XOR}$ Addition with of $X$ and the current state of Round Key of Block Size $b$

Odd Round Key Generation

• Odd Round Key $i$ is generated in a bijective manner from the previous even round key $(i-1)$ the following way